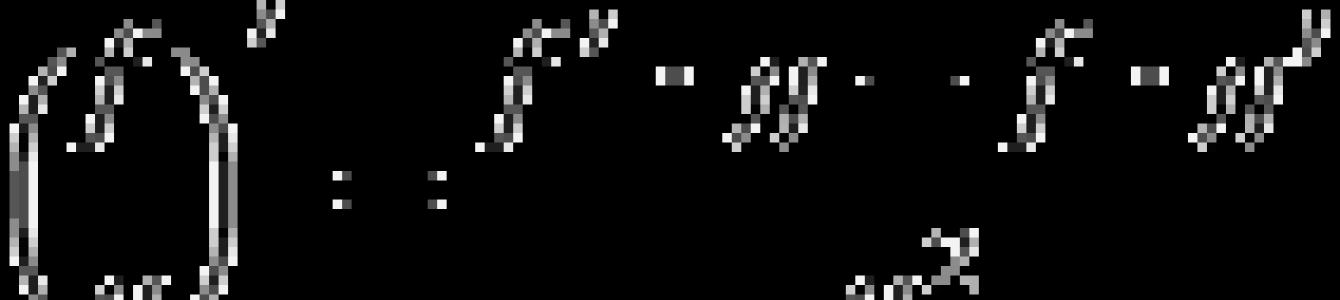Якщо йти за визначенням, то похідна функції в точці - це границя відношення приросту функції Δ y до приросту аргументу Δ x:
Начебто все зрозуміло. Але спробуйте порахувати за цією формулою, скажімо, похідну функції f(x) = x 2 + (2x + 3) · e x · sin x. Якщо все робити за визначенням, то через пару сторінок обчислень ви просто заснете. Тому існують простіші й ефективніші способи.
Для початку зауважимо, що з усього різноманіття функцій можна виділити так звані елементарні функції. Це відносно прості вирази, похідні яких давно обчислені і занесені в таблицю. Такі функції досить просто запам'ятати - разом з їх похідними.
Похідні елементарних функцій
Елементарні функції - це все, що перераховано нижче. Похідні цих функцій треба знати напам'ять. Тим більше що завчити їх зовсім нескладно - на те вони і елементарні.
Отже, похідні елементарних функцій:
| Назва | функція | похідна |
| Константа | f(x) = C, C ∈ R | 0 (так-так, нуль!) |
| Ступінь з раціональним показником | f(x) = x n | n · x n − 1 |
| синус | f(x) \u003d Sin x | cos x |
| косинус | f(x) \u003d Cos x | - sin x (Мінус синус) |
| тангенс | f(x) \u003d Tg x | 1 / cos 2 x |
| котангенс | f(x) \u003d Ctg x | - 1 / sin 2 x |
| натуральний логарифм | f(x) \u003d Ln x | 1/x |
| довільний логарифм | f(x) \u003d Log a x | 1/(x · ln a) |
| показова функція | f(x) = e x | e x (нічого не змінилося) |
Якщо елементарну функцію помножити на довільну постійну, то похідна нової функції теж легко вважається:
(C · f)’ = C · f ’.
Загалом, константи можна виносити за знак похідної. наприклад:
(2x 3) '\u003d 2 · ( x 3) '\u003d 2 · 3 x 2 = 6x 2 .
Очевидно, елементарні функції можна складати один з одним, множити, ділити - і багато іншого. Так з'являться нові функції, вже не особливо елементарні, але теж диференціюються за певними правилами. Ці правила розглянуті нижче.
Похідна суми і різниці
Нехай дано функції f(x) і g(x), Похідні яких нам відомі. Наприклад, можна взяти елементарні функції, які розглянуті вище. Тоді можна знайти похідну суми і різниці цих функцій:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
Отже, похідна суми (різниці) двох функцій дорівнює сумі (різниці) похідних. Доданків може бути більше. Наприклад, ( f + g + h)’ = f ’ + g ’ + h ’.
Строго кажучи, в алгебрі не існує поняття «віднімання». Є поняття «негативний елемент». Тому різниця f − g можна переписати як суму f + (-1) · g, І тоді залишиться лише одна формула - похідна суми.
f(x) = x 2 + sin x; g(x) = x 4 + 2x 2 − 3.
функція f(x) - це сума двох елементарних функцій, тому:
f ’(x) = (x 2 + sin x)’ = (x 2) '+ (sin x)’ = 2x + Cos x;
Аналогічно міркуємо для функції g(x). Тільки там вже три доданків (з точки зору алгебри):
g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).
відповідь:
f ’(x) = 2x + Cos x;
g ’(x) = 4x · ( x
2 + 1).
похідна твори
Математика - наука логічна, тому багато хто вважає, що якщо похідна суми дорівнює сумі похідних, то похідна твори strike"\u003e Дорівнює добутку похідних. А ось фіг вам! Похідна твори вважається зовсім за іншою формулою. А саме:
(f · g) ’ = f ’ · g + f · g ’
Формула нескладна, але її часто забувають. І не тільки школярі, а й студенти. Результат - неправильно вирішені завдання.
Завдання. Знайти похідні функцій: f(x) = x 3 · cos x; g(x) = (x 2 + 7x - 7) · e x .
функція f(x) Являє собою добуток двох елементарних функцій, тому все просто:
f ’(x) = (x 3 · cos x)’ = (x 3) '· cos x + x 3 · (cos x)’ = 3x 2 · cos x + x 3 · (- sin x) = x 2 · (3cos x − x · sin x)
У функції g(x) Перший множник трохи складніша, але загальна схема від цього не змінюється. Очевидно, перший множник функції g(x) Являє собою многочлен, і його похідна - це похідна суми. маємо:
g ’(x) = ((x 2 + 7x - 7) · e x)’ = (x 2 + 7x - 7) '· e x + (x 2 + 7x - 7) · ( e x)’ = (2x + 7) · e x + (x 2 + 7x - 7) · e x = e x · (2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x + 9) · e x .
відповідь:
f ’(x) = x 2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e
x
.
Зверніть увагу, що на останньому кроці похідна розкладається на множники. Формально цього робити не потрібно, однак більшість похідних обчислюються не самі по собі, а щоб дослідити функцію. А значить, далі похідна буде прирівнюватися до нуля, будуть з'ясовуватися її знаки і так далі. Для такої справи краще мати вираз, розкладене на множники.
Якщо є дві функції f(x) і g(x), Причому g(x) ≠ 0 на який нас цікавить безлічі, можна визначити нову функцію h(x) = f(x)/g(x). Для такої функції теж можна знайти похідну:
Неслабо, так? Звідки взявся мінус? чому g 2? А ось так! Це одна з найскладніших формул - без пляшки не розберешся. Тому краще вивчати її на конкретних прикладах.
Завдання. Знайти похідні функцій:
У чисельнику і знаменнику кожного дробу стоять елементарні функції, тому все, що нам потрібно - це формула похідної приватного:
За традицією, розкладемо чисельник на множники - це значно спростить відповідь:
Складна функція - це не обов'язково формула довжиною в півкілометра. Наприклад, досить взяти функцію f(x) \u003d Sin x і замінити змінну x, Скажімо, на x 2 + ln x. вийде f(x) \u003d Sin ( x 2 + ln x) - це і є складна функція. У неї теж є похідна, однак знайти її за правилами, розглянутими вище, не вийде.
Як бути? У таких випадках допомагає заміна змінної та формула похідної складної функції:
f ’(x) = f ’(t) · t ', Якщо x замінюється на t(x).
Як правило, з розумінням цієї формули справи ще більш сумно, ніж з похідною приватного. Тому її теж краще пояснити на конкретних прикладах, з докладним описом кожного кроку.
Завдання. Знайти похідні функцій: f(x) = e 2x + 3 ; g(x) \u003d Sin ( x 2 + ln x)
Зауважимо, що якщо в функції f(x) Замість виразу 2 x + 3 буде просто x, То вийде елементарна функція f(x) = e x . Тому робимо заміну: нехай 2 x + 3 = t, f(x) = f(t) = e t . Шукаємо похідну складної функції за формулою:
f ’(x) = f ’(t) · t ’ = (e t)’ · t ’ = e t · t ’
А тепер - увага! Виконуємо зворотну заміну: t = 2x + 3. Отримаємо:
f ’(x) = e t · t ’ = e 2x + 3 · (2 x + 3)’ = e 2x + 3 · 2 \u003d 2 · e 2x + 3
Тепер розберемося з функцією g(x). Очевидно, треба замінити x 2 + ln x = t. маємо:
g ’(x) = g ’(t) · t '\u003d (Sin t)’ · t '\u003d Cos t · t ’
Зворотній заміна: t = x 2 + ln x. тоді:
g ’(x) \u003d Cos ( x 2 + ln x) · ( x 2 + ln x) '\u003d Cos ( x 2 + ln x) · (2 x + 1/x).
От і все! Як видно з останнього виразу, вся задача звелася до обчислення похідної суми.
відповідь:
f ’(x) \u003d 2 · e
2x + 3 ;
g ’(x) = (2x + 1/x) · Cos ( x 2 + ln x).
Дуже часто на своїх уроках замість терміна «похідна» я використовую слово «штрих». Наприклад, штрих від суми дорівнює сумі штрихів. Так зрозуміліше? Ну от і добре.
Таким чином, обчислення похідної зводиться до позбавлення від цих самих штрихів за правилами, розглянутим вище. Як останній приклад повернемося до похідної ступеня з раціональним показником:
(x n)’ = n · x n − 1
Мало хто знає, що в ролі n цілком може виступати дробове число. Наприклад, корінь - це x 0,5. А що, якщо під коренем буде стояти щось неймовірне? Знову вийде складна функція - такі конструкції люблять давати на контрольних роботах та іспитах.
Завдання. Знайти похідну функції:
Для початку перепишемо корінь у вигляді ступеня з раціональним показником:
f(x) = (x 2 + 8x − 7) 0,5 .
Тепер робимо заміну: нехай x 2 + 8x − 7 = t. Знаходимо похідну за формулою:
f ’(x) = f ’(t) · t ’ = (t 0,5) '· t '\u003d 0,5 · t -0,5 · t ’.
Робимо зворотну заміну: t = x 2 + 8x - 7. Маємо:
f ’(x) \u003d 0,5 · ( x 2 + 8x - 7) -0,5 · ( x 2 + 8x - 7) '\u003d 0,5 · (2 x + 8) · ( x 2 + 8x − 7) −0,5 .
Нарешті, повертаємося до коренів:
Вирішувати фізичні завдання або приклади з математики абсолютно неможливо без знань про похідну і методах її обчислення. Похідна - одне з найважливіших понять математичного аналізу. Цією фундаментальною темі ми і вирішили присвятити сьогоднішню статтю. Що таке похідна, який її фізичний та геометричний зміст, як порахувати похідну функції? Всі ці питання можна об'єднати в один: як зрозуміти похідну?
Геометричний і фізичний зміст похідної
Нехай є функція f (x) , Задана в деякому інтервалі (A, b) . Точки х і х0 належать цьому інтервалу. При зміні х змінюється і сама функція. Зміна аргументу - різниця його значень х-х0 . Ця різниця записується як дельта ікс і називається приростом аргументу. Зміною або збільшенням функції називається різниця значень функції в двох точках. Визначення похідної:
Похідна функції в точці - границя відношення приросту функції в даній точці до приросту аргументу, коли останній прямує до нуля.
Інакше це можна записати так:

Який сенс в знаходженні такої межі? А ось який:
похідна від функції в точці дорівнює тангенсу кута між віссю OX і дотичної до графіка функції в даній точці.

Фізичний зміст похідної: похідна шляху по часу дорівнює швидкості прямолінійного руху.
Дійсно, ще зі шкільних часів всім відомо, що швидкість - це приватна шляху x \u003d f (t) і часу t . Середня швидкість за певний проміжок часу:

Щоб дізнатися швидкість руху в момент часу t0 потрібно обчислити межа:

Правило перше: виносимо константу
Константу можна винести за знак похідної. Більш того - це потрібно робити. При вирішенні прикладів з математики візьміть за правило - якщо можете спростити вираз, обов'язково спрощуйте .
Приклад. Обчислимо похідну:

Правило друге: похідна суми функцій
Похідна суми двох функцій дорівнює сумі похідних цих функцій. Те ж саме справедливо і для похідної різниці функцій.

Не будемо наводити доведення цієї теореми, а краще розглянемо практичний приклад.
Знайти похідну функції:


Правило третє: похідна добутку функцій
Похідна добутку двох диференційовних функцій обчислюється за формулою:

Приклад: знайти похідну функції:

Рішення: 
Тут важливо сказати про обчисленні похідних складних функцій. Похідна складної функції дорівнює добутку похідної цієї функції по проміжному аргументу на похідну проміжного аргументу по незалежній змінній.
У вищевказаному прикладі ми зустрічаємо вираз:

В даному випадку проміжний аргумент - 8х в п'ятого ступеня. Для того, щоб обчислити похідну такого виразу спочатку вважаємо похідну зовнішньої функції з проміжного аргументу, а потім множимо на похідну безпосередньо самого проміжного аргументу по незалежній змінній.
Правило четверте: похідна приватного двох функцій
Формула для визначення похідної від приватного двох функцій:



Ми постаралися розповісти про похідні для чайників з нуля. Ця тема не так проста, як здається, тому попереджаємо: в прикладах часто зустрічаються пастки, так що будьте уважні при обчисленні похідних.
З будь-яким питанням з цієї та інших тем ви можете звернутися в студентський сервіс. За короткий термін ми допоможемо вирішити найскладнішу контрольну і розібратися з завданнями, навіть якщо ви ніколи раніше не займалися обчисленням похідних.
обчислення похідної - одна з найважливіших операцій в диференціальному обчисленні. Нижче наводиться таблиця знаходження похідних простих функцій. Більш складні правила диференціювання дивіться в інших уроках:- Таблиця похідних експоненційних і логарифмічних функцій
Похідні простих функцій
1. Похідна від числа дорівнює нулюс'\u003d 0
приклад:
5'\u003d 0
пояснення:
Похідна показує швидкість зміни значення функції при зміні аргументу. Оскільки число не змінюється ні за яких умов - швидкість його зміни завжди дорівнює нулю.
2. похідна змінної дорівнює одиниці
x'\u003d 1
пояснення:
При кожному збільшенні аргументу (х) на одиницю значення функції (результату обчислень) збільшується на цю ж саму величину. Таким чином, швидкість зміни значення функції y \u003d x точно дорівнює швидкості зміни значення аргументу.
3. Похідна змінної і множника дорівнює цьому множнику
сx' \u003d з
приклад:
(3x) '\u003d 3
(2x) '\u003d 2
пояснення:
В даному випадку, при кожній зміні аргументу функції ( х) Її значення (y) зростає в з раз. Таким чином, швидкість зміни значення функції по відношенню до швидкості зміни аргументу точно дорівнює величині з.
Звідки випливає, що
(Cx + b) "\u003d c
тобто диференціал лінійної функції y \u003d kx + b дорівнює кутовому коефіцієнту нахилу прямої (k).
4. Похідна змінної по модулю дорівнює приватному цієї змінної до її модулю
| X | "\u003d X / | x | за умови, що х ≠ 0
пояснення:
Оскільки похідна змінної (див. Формулу 2) дорівнює одиниці, то похідна модуля відрізняється лише тим, що значення швидкості зміни функції змінюється на протилежне при перетині точки початку координат (спробуйте намалювати графік функції y \u003d | x | і переконайтеся в цьому самі. Саме таке значення і повертає вираз x / | x |. Коли x< 0 оно равно (-1), а когда x > 0 - одиниці. Тобто при негативних значеннях змінної х при кожному збільшенні зміні аргументу значення функції зменшується на точно таке ж значення, а при позитивних - навпаки, зростає, але точно на таке ж значення.
5. Похідна змінної в ступеня дорівнює добутку числа цього ступеня і змінної в ступеня, зменшеної на одиницю
(X c) "\u003d cx c-1, За умови, що x c і СX c-1, визначені а з ≠ 0
приклад:
(X 2) "\u003d 2x
(X 3) "\u003d 3x 2
Для запам'ятовування формули:
Знесіть ступінь змінної "вниз" як множник, а потім зменшіть саму ступінь на одиницю. Наприклад, для x 2 - двійка виявилася попереду ікси, а потім зменшена ступінь (2-1 \u003d 1) просто дала нам 2х. Те ж саме відбулося для x 3 - трійку "спускаємо вниз", зменшуємо її на одиницю і замість куба маємо квадрат, тобто 3x 2. Трохи »не науково", але дуже просто запам'ятати.
6. похідна дроби 1 / х
(1 / х) "\u003d - 1 / x 2
приклад:
Оскільки дріб можна представити як зведення в негативну ступінь
(1 / x) "\u003d (x -1)", тоді можна застосувати формулу з правила 5 таблиці похідних
(X -1) "\u003d -1x -2 \u003d - 1 / х 2
7. похідна дроби зі змінною довільного ступеня в знаменнику
(1 / x c) "\u003d - c / x c + 1
приклад:
(1 / x 2) "\u003d - 2 / x 3
8. похідна кореня (Похідна змінної під квадратним коренем)
(√x) "\u003d 1 / (2√x) або 1/2 х -1/2
приклад:
(√x) "\u003d (х 1/2)" означає можна застосувати формулу з правила 5
(Х 1/2) "\u003d 1/2 х -1/2 \u003d 1 / (2√х)
9. Похідна змінної під коренем довільного ступеня
(N √x) "\u003d 1 / (n n √x n-1)
Операція відшукання похідної називається диференціюванням.
В результаті рішення задач про відшукання похідних у найпростіших (і не дуже простих) функцій по визначенню похідною як межі відношення приросту до приросту аргументу з'явилися таблиця похідних і точно певні правила диференціювання. Першими на ниві знаходження похідних потрудилися Ісаак Ньютон (1643-1727) і Готфрід Вільгельм Лейбніц (1646-1716).
Тому в наш час, щоб знайти похідну будь-якої функції, не треба обчислювати згаданий вище границя відношення приросту функції до приросту аргументу, а потрібно лише скористатися таблицею похідних і правилами диференціювання. Для знаходження похідної підходить наступний алгоритм.
Щоб знайти похідну, Треба вираз під знаком штриха розібрати на складові прості функції і визначити, якими діями (Твір, сума, приватне) пов'язані ці функції. Далі похідні елементарних функцій знаходимо в таблиці похідних, а формули похідних твори, суми і приватного - в правилах диференціювання. Таблиця похідних і правила диференціювання дані після перших двох прикладів.
Приклад 1. Знайти похідну функції
Рішення. З правил диференціювання з'ясовуємо, що похідна суми функцій є сума похідних функцій, т. Е.
З таблиці похідних з'ясовуємо, що похідна "ікси" дорівнює одиниці, а похідна синуса - косинусу. Підставляємо ці значення в суму похідних і знаходимо необхідну умовою завдання похідну:
Приклад 2. Знайти похідну функції
Рішення. Диференціюючи як похідну суми, в якій другий доданок з постійним множником, його можна винести за знак похідної:
![]()
Якщо поки виникають питання, звідки що береться, вони, як правило, прояснюються після ознайомлення з таблицею похідних і найпростішими правилами диференціювання. До них ми і переходимо прямо зараз.
Таблиця похідних простих функцій
| 1. Похідна константи (числа). Будь-якого числа (1, 2, 5, 200 ...), яке є в вираженні функції. Завжди дорівнює нулю. Це дуже важливо пам'ятати, так як потрібно дуже часто | |
| 2. Похідна незалежної змінної. Найчастіше "ікси". Завжди дорівнює одиниці. Це теж важливо запам'ятати надовго | |
| 3. Похідна ступеня. В ступінь при вирішенні задач потрібно перетворювати неквадратні коріння. | |
| 4. Похідна змінної в ступені -1 | |
| 5. Похідна квадратного кореня | |
| 6. Похідна синуса | |
| 7. Похідна косинуса | |
| 8. Похідна тангенса | |
| 9. Похідна котангенс | |
| 10. Похідна арксинуса | |
| 11. Похідна арккосинуса | |
| 12. Похідна арктангенса | |
| 13. Похідна арккотангенса | |
| 14. Похідна натурального логарифма | |
| 15. Похідна логарифмічної функції | |
| 16. Похідна експоненти | |
| 17. Похідна показовою функції |
Правила диференціювання
| 1. Похідна суми або різниці | |
| 2. Похідна твори | |
| 2a. Похідна вираження, помноженого на постійний множник | |
| 3. Похідна приватного | |
| 4. Похідна складної функції |  |
Правило 1. якщо функції
діфференцируєми в деякій точці, то в тій же точці мають похідні і функції
причому
![]()
тобто похідна алгебраїчної суми функцій дорівнює алгебраїчній сумі похідних цих функцій.
Слідство. Якщо дві диференціюються відрізняються на постійний доданок, то їх похідні рівні, Тобто
Правило 2.якщо функції
діфференцируєми в деякій точці, то в той же точці дифференцируемого і їх твір
причому
![]()
тобто похідна добутку двох функцій дорівнює сумі творів кожної з цих функцій на похідну інший.
Слідство 1. Постійний множник можна виносити за знак похідної:
Слідство 2. Похідна твори кількох диференціюються дорівнює сумі творів похідною кожного із співмножників на всі інші.
Наприклад, для трьох множників:
Правило 3.якщо функції
діфференцируєми в деякій точці і , то в цій точці дифференцируемого і їхня приватнаu / v, причому
![]()
тобто похідна приватного двох функцій дорівнює дробу, чисельник якого є різниця творів знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат колишнього чисельника.
Де що шукати на інших сторінках
При знаходженні похідної добутку і частки в реальних задачах завжди потрібно застосовувати відразу кілька правил диференціювання, тому більше прикладів на ці похідні - в статті"Похідна добутку і частки функцій".
Зауваження.Слід не плутати константу (тобто, число) як доданок в сумі і як постійний множник! У разі доданка її похідна дорівнює нулю, а в разі постійного множника вона виноситься за знак похідних. Це типова помилка, яка зустрічається на початковому етапі вивчення похідних, але в міру рішення вже декількох одно- двоскладові прикладів середній студент цієї помилки вже не робить.
А якщо при диференціюванні твори або приватного у вас з'явилося доданок u"v , в якому u - число, наприклад, 2 або 5, тобто константа, то похідна цього числа буде дорівнює нулю і, отже, все доданок дорівнюватиме нулю (такий випадок розібраний в прикладі 10).
інша часта помилка - механічне рішення похідною складної функції як похідною простої функції. Тому похідною складної функції присвячена окрема стаття. Але спочатку будемо вчитися знаходити похідні простих функцій.
По ходу не обійтися без перетворень виразів. Для цього може знадобитися відкрити в нових вікнах посібники Дії зі ступенями і корінням і Дії з дробами .
Якщо Ви шукаєте рішення похідних дробів зі ступенями і корінням, тобто, коли функція має вигляд начебто ![]() , То йдіть на заняття "Похідна суми дробів зі ступенями і корінням".
, То йдіть на заняття "Похідна суми дробів зі ступенями і корінням".
Якщо ж перед Вами завдання на зразок ![]() , То Вам на заняття "Похідні простих тригонометричних функцій".
, То Вам на заняття "Похідні простих тригонометричних функцій".
Покрокові приклади - як знайти похідну
Приклад 3. Знайти похідну функції
Рішення. Визначаємо частини виразу функції: все вираз являє твір, а його співмножники - суми, в другій з яких одна з складових містить постійний множник. Застосовуємо правило диференціювання твори: похідна добутку двох функцій дорівнює сумі творів кожної з цих функцій на похідну інший:
![]()
Далі застосовуємо правило диференціювання суми: похідна алгебраїчної суми функцій дорівнює алгебраїчній сумі похідних цих функцій. У нашому випадку в кожній сумі другий доданок зі знаком мінус. У кожній сумі бачимо і незалежну змінну, похідна якої дорівнює одиниці, і константу (число), похідна якої дорівнює нулю. Отже, "ікс" у нас перетворюється в одиницю, а мінус 5 - в нуль. У другому вираженні "ікс" помножений на 2, так що двійку множимо на ту ж одиницю як похідну "ікси". Отримуємо наступні значення похідних:
Підставляємо знайдені похідні в суму творів і отримуємо необхідну умовою завдання похідну всієї функції:
![]()
Приклад 4. Знайти похідну функції
Рішення. Від нас вимагається знайти похідну приватного. Застосовуємо формулу диференціювання приватного: похідна приватного двох функцій дорівнює дробу, чисельник якого є різниця творів знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат колишнього чисельника. отримуємо:

Похідну сомножителей в чисельнику ми вже знайшли в прикладі 2. Не забудемо також, що твір, що є другим співмножником в чисельнику в поточному прикладі береться зі знаком мінус:

Якщо Ви шукаєте рішення таких задач, в яких треба знайти похідну функції, де суцільне нагромадження коренів і ступенів, як, наприклад, ![]() , То ласкаво просимо на заняття "Похідна суми дробів зі ступенями і корінням" .
, То ласкаво просимо на заняття "Похідна суми дробів зі ступенями і корінням" .
Якщо ж Вам потрібно дізнатися більше про похідні синусів, косинусів, тангенсів і інших тригонометричних функцій, тобто, коли функція має вигляд начебто ![]() , То Вам на урок "Похідні простих тригонометричних функцій" .
, То Вам на урок "Похідні простих тригонометричних функцій" .
Приклад 5. Знайти похідну функції
Рішення. У даній функції бачимо твір, один із співмножників яких - квадратний корінь з незалежною змінною, з похідною якого ми ознайомилися в таблиці похідних. За правилом диференціювання твори і табличному значенню похідної квадратного кореня отримуємо:

Приклад 6. Знайти похідну функції
Рішення. У даній функції бачимо приватне, ділене якого - квадратний корінь з незалежної змінної. За правилом диференціювання приватного, яке ми повторили і застосували в прикладі 4, і табличному значенню похідної квадратного кореня отримуємо:

Щоб позбутися від дробу в чисельнику, множимо чисельник і знаменник на.
Походження диференціального обчислення викликано необхідністю вирішувати певні фізичні завдання. Передбачається, що людина, що володіє диференціальним численням, може брати похідні від різних функцій. Чи вмієте ви брати похідну від функції, вираженої дробом?
Інструкція
1. Будь-яка дріб має чисельник і знаменник. У процесі знаходження похідної від дроби знадобиться знаходити окремо похідну чисельника і похідну знаменника.
2. щоб виявити похідну від дроби , похідну чисельника домножьте на знаменник. Відніміть з отриманого виразу похідну знаменника, помножену на чисельник. Підсумок поділіть на знаменник в квадраті.
3. Приклад 1 '\u003d / cos? (X) \u003d / cos? (X) \u003d / cos? (X) \u003d 1 / cos? (X).
4. Отриманий результат є нічим іншим, як табличним значенням похідної функції тангенса. Воно й зрозуміло, чай відношення синуса до косинусу і є, за визначенням, тангенс. Виходить, tg (x) \u003d '\u003d 1 / cos? (X).
5. Приклад 2 [(x? - 1) / 6x] '\u003d [(2x · 6x - 6 · x?) / 6?] \u003d / 36 \u003d 6x? / 36 \u003d x? / 6.
6. окремим випадком дроби є така дріб, у якої в знаменнику одиниця. виявити похідну від такого виду дроби простіше: досить уявити її у вигляді знаменника зі ступенем (-1).
7. Приклад (1 / x) '\u003d' \u003d -1 · x ^ (- 2) \u003d -1 / x ?.
Зверніть увагу!
Дріб може містити в своєму складі ще кілька дробів. В такому випадку комфортніше знаходити спочатку окремо похідні «первинних» дробів.
Корисна порада
Коли ви шукайте похідні знаменника і чисельника, застосовуйте правила диференціювання: суми, твори, важких функцій. Придатне утримувати в голові похідні найпростіших табличних функцій: лінійної, показовою, статечної, логарифмічною, тригонометричних і т.д.